Nagyobb számú adatot (n > 50) célszerű csoportosítással áttekinthetőbbé tenni, osztályokba sorolni. Erre vonatkozóan praktikus tanácsként n/10 darab osztály megadása javasolható. Az osztályok legyenek egyenlő hosszúságú intervallumok az adatok halmazán.

Egy osztály (jelölje: i) adatainak számát az adott osztály abszolút gyakoriságának nevezzük. Jele f_i, amelyben az f betű az angol frequency (gyakoriság) szó kezdőbetűjére, az i pedig az említett osztályra utal. Amennyiben az f_i gyakoriságot az adatok számához (n) viszonyítjuk, akkor i osztály relatív (százalékos) gyakoriságát kapjuk:

f(%)_i = 100f_i/n

Az osztály felső és alsó szélét (névleges) osztályhatárnak (OH) hívjuk. Az osztályközép (OK) a két érték (OH) számtani közepe. Ha minden osztályt úgy bővítünk, hogy az osztályok éppen összeérnek, akkor a valódi osztályhatárokat (VOH) kapjuk. Az osztályszélesség a valódi osztályhatárok távolsága.

A gyakorisági eloszlás az osztályokat, osztályközepeket, valamint a gyakoriságokat összefoglaló táblázatot jelenti. Mindent egybevetve könnyen látható, hogy egy mintához több gyakorisági eloszlás is megadható. Az úgynevezett kumulatív (összegzett) gyakoriságokat úgy kapjuk, hogy a gyakoriságokat (relatív gyakoriságokat) fokozatosan, fokonként összegezzük.

A gyakorisági eloszlást ábrázolhatjuk kétdimenziós koordináta-rendszerben. Amennyiben – az adatok tengelyén megadott – osztályközepek fölött az adott osztály gyakoriságát (százalékos gyakoriságát) jelentő magasságban pontokat teszünk, majd azokat összekötjük, akkor az úgynevezett gyakorisági poligont rajzoljuk meg.

A hisztogram (oszlopdiagram) pedig úgy készíthető, hogy az adatok tengelyén levő osztályok fölé az egyes osztályok gyakoriságának megfelelő magasságú oszlopokat rajzolunk.

A következőkben a kvantiliseket értelmezzük. Bármely 0 < p < 1 valós számra a gyakorisági eloszlás p-kvantilisén (Q_p) az adatok tengelyén azt az értéket értjük, amely a minta adatainak kereken p-ed részénél nagyobb; vagyis (1-p)-ed részénél kisebb. Mondhatjuk azt is, amennyiben az adatok az egyes osztályokban egyenletesen oszlanak el az osztályhatárok között, akkor a hisztogram területét a p : (1-p) arányban osztja az adatok tengelyére a Q_p pontban emelt merőleges.

A Q_p-t kvartilisnek nevezzük, ha p egész számú többszöröse az egynegyednek. Következőleg egy minta három különböző kvartilisét értelmezhetjük: Q_0,25, Q_0,5 és Q_0,75.

A statisztikai sokaság mérete általánosságban nagy, ezért fontos, hogy néhány számmal jól tudjuk jellemezni az adatokat. Ezek a számok a statisztikai mutatók.

A legismertebb statisztikai mutató az átlag: a számsokaság összegét elosztjuk a számsokaság darabszámával.

A minta átlaga tehát az adatok számtani közepe:

Gyakorisági eloszlásnál minden adatot a megfelelő osztály osztályközepe képvisel. Ha y₁, y₂, …, y_k az osztályközepek és f₁, f₂, …, f_k a megfelelő gyakoriságok, akkor:

Az eloszlás (a minta) módusza (jele: Mo) a minta legnagyobb gyakoriságú értéke, ami osztálybesorolás esetén a legnagyobb gyakoriságú osztály osztályközepe az eloszlásban. A móduszt akkor célszerű használni, ha az adatok közül egyet emel ki. Amennyiben a sokaságban több adat is csaknem megegyező gyakoriságú, akkor nem praktikus a használata.

Az eloszlás (a minta) mediánja (jele: Me) a Q_0,5 kvartilis: ennél az értéknél a minta adatainak pontosan 50%-a kisebb, s 50%-a nagyobb. Ha az adatok nem gyakorisági eloszlással adottak, akkor a medián páratlan adatszám esetén a nagyság szerint rendezett adatok közül a középső, páros számú adatnál pedig a két középső számtani közepe.

A sokaságok jellemzésére nem elegendő csupán a középértékeket használni. Helyénvaló a szóródást mérő számok közlése. A minta szórtságát jellemző legegyszerűbb mérőszám a szóródási terjedelem.

A terjedelem (T) a minta legnagyobb és legkisebb elemének különbsége:

T = x_max – x_min.

A gyakorisági eloszlásból kiindulva a terjedelem a legnagyobb osztály valódi felső osztályhatárának és a legkisebb osztály valódi alsó osztályhatárának a különbsége.

Mivel a terjedelem egyszerűen számolható, használata gyakori. Ugyanakkor már egyetlen szélsőséges adat nagymértékben befolyásolja az értékét. Az interkvartilis félterjedelem (IF) nagyságát a szélső értékek nem befolyásolják, mert azt a minta középső adatainak a középértéktől vett eltérése határozza meg.

Az interkvartilis félterjedelem (IF) a harmadik és első kvartilis különbségének a fele:

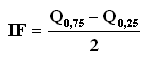
A minta elemeinek eloszlását jellemző szórás értelmezése a következőképpen lehetséges. Induljunk ki az x₁, x₂, …, x_nelemekből álló n elemű minta úgynevezett négyzetes összegéből:

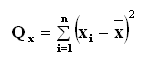
Ennek felhasználásával a minta szórásnégyzete, varianciája:

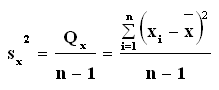
A minta szórása így a következő:

ahol n-1 a szórás szabadságfoka.

A szórás egy számítási módja ebből egyszerű átalakításokkal kapható:

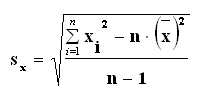
A szórás gyakorisági eloszlást felhasználva is könnyen meghatározható. Jelölje rendre y₁, y₂, …, y_k az osztályközepeket, s a megfelelő gyakoriságok legyenek f₁, f₂, …, f_k.

A szórás ekkor az alábbi módon számolható ki:

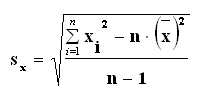
A hiba jelentése a pontos értéktől való eltérés. Egy minta hibáját az adatoknak az átlagtól való eltérése adja, amelynek mértéke a szórás. További elnevezések: a szórás az átlagos eltérés; a kétszeres szórás a hibakorlát, a „legnagyobb eltérés”; a háromszoros szórás pedig a biztos hibakorlát.

A mintát a populációból vesszük, amelynek a paramétereit nem ismerjük. Ezért a populáció középértékét a minta átlagával közelítjük. A populáció középértékétől való eltérését a populáció adatainak pedig a szórással becsüljük.

Könnyű belátni, hogy a mintát reprezentáló átlag hibája, vagyis az átlag szórása (jele s_x) határozottan kisebb az értékei hibájánál:

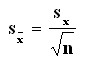
Mivel a szórás segítségével csak azonos értéktartományú minták szóródása vethető össze, az összehasonlíthatóság lehetőségének a megteremtésére bevezetett mutató a variációs együttható (relatív szórás). A variációs együttható a minta szórását a minta átlagához viszonyítja:

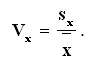
A V_x tehát mértékegység nélküli szám. Megjegyezzük még, hogy a minta állandóságára következtethetünk valahányszor 0 ≤ V_x < 0,1, ekkor a minta homogén. A minta változékony, ha 0,1 ≤ V_x < 0,3. Végül a minta igen erősen változékony, erősen ingadozik, amikor 0,3 ≤ V_x.